TEM: AEMR TEM-FAST 48 system#

In this example we compute the TEM response from the TEM-FAST 48 system.

This example was contributed by Lukas Aigner (@aignerlukas), who was interested in modelling the TEM-FAST system, which is used at the TU Wien. If you are interested and want to use this work please have a look at the corresponding paper Aigner et al. (2024).

The modeller empymod models the electromagnetic (EM) full wavefield Greens function for electric and magnetic point sources and receivers. As such, it can model any EM method from DC to GPR. However, how to actually implement a particular EM method and survey layout can be tricky, as there are many more things involved than just computing the EM Greens function.

References

Aigner, L., D. Werthmüller, and A. Flores Orozco, 2024, Sensitivity analysis of inverted model parameters from transient electromagnetic measurements affected by induced polarization effects; Journal of Applied Geophysics, Volume 223, Pages 105334, doi: 10.1016/j.jappgeo.2024.105334.

import empymod
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')

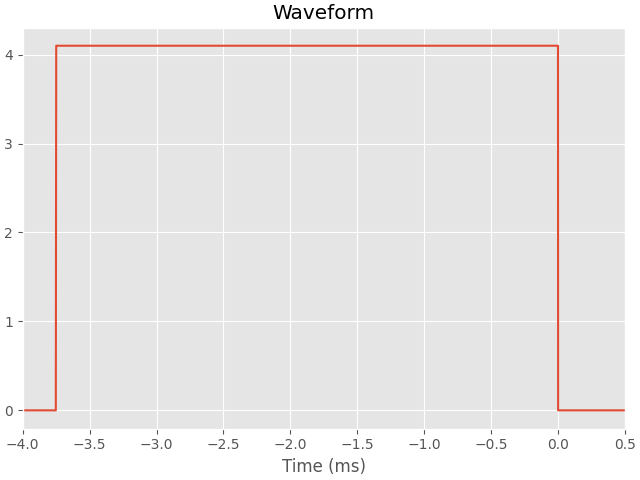
1. TEM-FAST 48 Waveform and other characteristics#

The TEM-FASt system uses a “time-key” value to determine the number of gates, the front ramp and the length of the current pulse. We are using values that correspond to a time-key of 5.

turn_on_ramp = -3e-6
turn_off_ramp = 0.95e-6
on_time = 3.75e-3

injected_current = 4.1  # Ampere
time_gates = np.array([
    4.060e+00, 5.070e+00, 6.070e+00, 7.080e+00,
    8.520e+00, 1.053e+01, 1.255e+01, 1.456e+01,
    1.744e+01, 2.146e+01, 2.549e+01, 2.950e+01,
    3.528e+01, 4.330e+01, 5.140e+01, 5.941e+01,  # time-key 1
    7.160e+01, 8.760e+01, 1.036e+02, 1.196e+02,  # time-key 2
    1.436e+02, 1.756e+02, 2.076e+02, 2.396e+02,  # time-key 3
    2.850e+02, 3.500e+02, 4.140e+02, 4.780e+02,  # time-key 4
    5.700e+02, 6.990e+02, 8.280e+02, 9.560e+02,  # time-key 5
]) * 1e-6  # from us to s

nodes = np.array([turn_on_ramp - on_time, -on_time, 0, turn_off_ramp])
amplitudes = np.array([0.0, injected_current, injected_current, 0.0])

fig, ax = plt.subplots(1, 1, constrained_layout=True)
ax.set_title('Waveform')
ax.plot(np.r_[-9, nodes*1e3, 2], np.r_[0, amplitudes, 0])
ax.set_xlabel('Time (ms)')
ax.set_xlim([-4, 0.5])

2. `empymod` implementation#

Here we collect the necessary input for empymod to model temfast.

# The waveform signal
signal = {'nodes': nodes, 'amplitudes': amplitudes, 'signal': 1}

# We model the square with 1/2 of one side. This makes it faster, but it
# will only work for a horizontal square loop, with a central receiver.
square_side = 12.5
hs = square_side / 2  # half side length

temfast = {
    "src": [hs, hs, 0, hs, 0, 0],  # El. dipole source; half of one side.
    "rec": [0, 0, 0, 0, 90],       # Receiver at the origin, vertical.
    "depth": [0, 8, 20],           # Interface depths.
    "freqtime": time_gates,        # Wanted times.
    "signal": signal,              # Signal.
    "mrec": "b",                   # It is an el. source, but a magn. rec.
    "strength": 8,                 # To account for 4 sides of square loop.
    "srcpts": 3,                   # Approx. the finite dip. with 3 points.
    "ftarg": {"dlf": "key_81_2009"},  # Shorter, faster filters.
    "htarg": {"dlf": "key_101_2009", "pts_per_dec": -1},
    "cutofffreq": 1e8,             # Determined empirically for TEM-FAST
}

def pelton_res(inp, p_dict):
    """ Pelton et al. (1978).
    code from: https://empymod.emsig.xyz/en/stable/examples/time_domain/
               cole_cole_ip.html#sphx-glr-examples-time-domain-cole-cole-ip-py
    """

    # Compute complex resistivity from Pelton et al.
    # print('\n   shape: p_dict["freq"]\n', p_dict['freq'].shape)
    iwtc = np.outer(2j*np.pi*p_dict['freq'], inp['tau'])**inp['c']

    rhoH = inp['res'] * (1 - inp['m']*(1 - 1/(1 + iwtc)))
    rhoV = rhoH*p_dict['aniso']**2

    # Add electric permittivity contribution
    etaH = 1/rhoH + 1j*p_dict['etaH'].imag
    etaV = 1/rhoV + 1j*p_dict['etaV'].imag

    return etaH, etaV

3. Computate responses#

rhos = [2e14, 25, 5, 50]

rhos_ip = {
    'res': rhos,
    'm': np.array([0, 0, 0.9, 0]),
    'tau': np.array([1e-7, 1e-6, 5e-4, 1e-6]),
    'c': np.array([0.01, 0, 0.9, 0]),
    'func_eta': pelton_res,
}

# Compute conductive model
response = empymod.bipole(res=rhos, **temfast)

# Compute conductive model
response_ip = empymod.bipole(res=rhos_ip, **temfast)

:: empymod END; runtime = 0:00:00.077319 :: 354 kernel call(s)

:: empymod END; runtime = 0:00:00.075175 :: 354 kernel call(s)

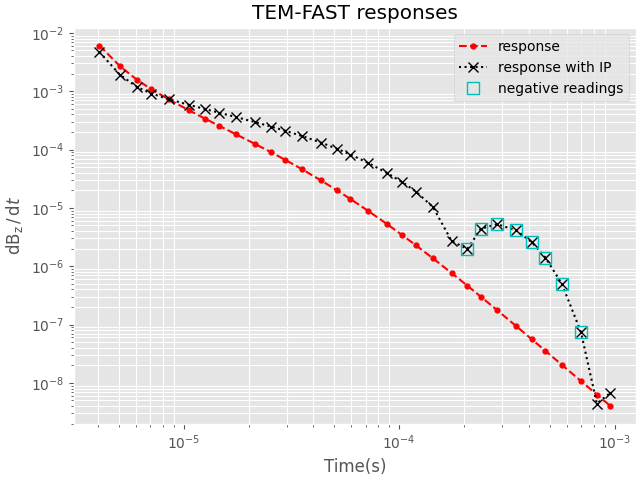
4. Comparison#

fig, ax = plt.subplots(1, 1, constrained_layout=True)

ax.set_title('TEM-FAST responses')

# empymod
ax.plot(time_gates, response, 'r.--', ms=7, label="response")
ax.plot(time_gates, abs(response_ip), 'kx:', ms=7, label="response with IP")

sub0 = response_ip[response_ip < 0]
tg_sub0 = time_gates[response_ip < 0]
ax.plot(tg_sub0, abs(sub0), marker='s', ls='none', mfc='none',
        ms=8, mew=1, mec='c', label="negative readings")

# Plot settings
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel("Time(s)")
ax.set_ylabel(r"$\mathrm{d}\mathrm{B}_\mathrm{z}\,/\,\mathrm{d}t$")
ax.grid(which='both')
ax.legend()

empymod.Report()

Tue Jan 27 22:10:44 2026 UTC
OS	Linux (Ubuntu 22.04)	CPU(s)	2	Machine	x86_64
Architecture	64bit	RAM	7.6 GiB	Environment	Python
File system	ext4
Python 3.11.12 (main, May 6 2025, 10:45:53) [GCC 11.4.0]
numpy	2.3.5	scipy	1.17.0	numba	0.63.1
empymod	2.5.5.dev12+g59de0f90f	libdlf	0.3.0	IPython	9.9.0
matplotlib	3.10.8